[ad_1]
Picture by Writer
Should you’re conversant in machine studying, you understand that knowledge factors within the knowledge set and the subsequently engineered options are all factors (or vectors) in an n-dimensional house.
The gap between any two factors additionally captures the similarity between them. Supervised studying algorithms comparable to Ok Nearest Neighbors (KNN) and clustering algorithms like Ok-Means Clustering use the notion of distance metrics to seize the similarity between knowledge factors.
In clustering, the evaluated distance metric is used to group knowledge factors collectively. Whereas, in KNN, this distance metric is used to search out the Ok closest factors to the given knowledge level.
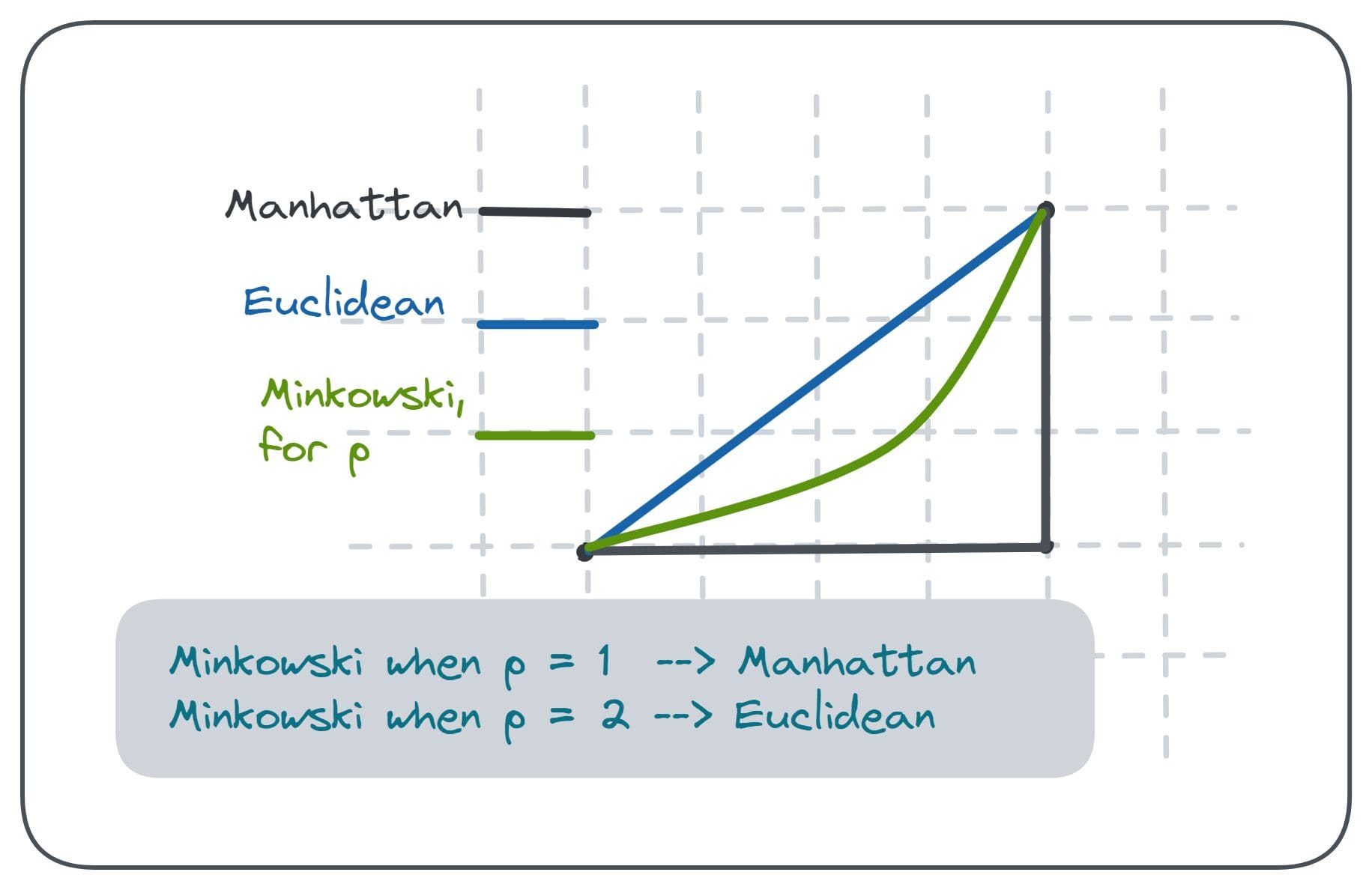
On this article, we’ll evaluation the properties of distance metrics after which take a look at probably the most generally used distance metrics: Euclidean, Manhattan and Minkowski. We’ll then cowl compute them in Python utilizing built-in capabilities from the scipy module.
Let’s start!
Earlier than we study in regards to the varied distance metrics, let’s evaluation the properties that any distance metric in a metric house ought to fulfill [1]:
1. Symmetry
If x and y are two factors in a metric house, then the gap between x and y needs to be equal to the gap between y and x.
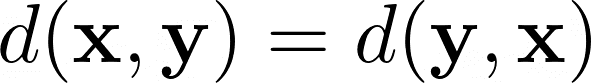
2. Non-negativity
Distances ought to all the time be non unfavorable. That means it needs to be higher than or equal to zero.

The above inequality holds with equality (d(x,y) = 0) if and provided that x and y denote the identical level, i.e., x = y.
3. Triangle Inequality
Given three factors x, y, and z, the gap metric ought to fulfill the triangle inequality:

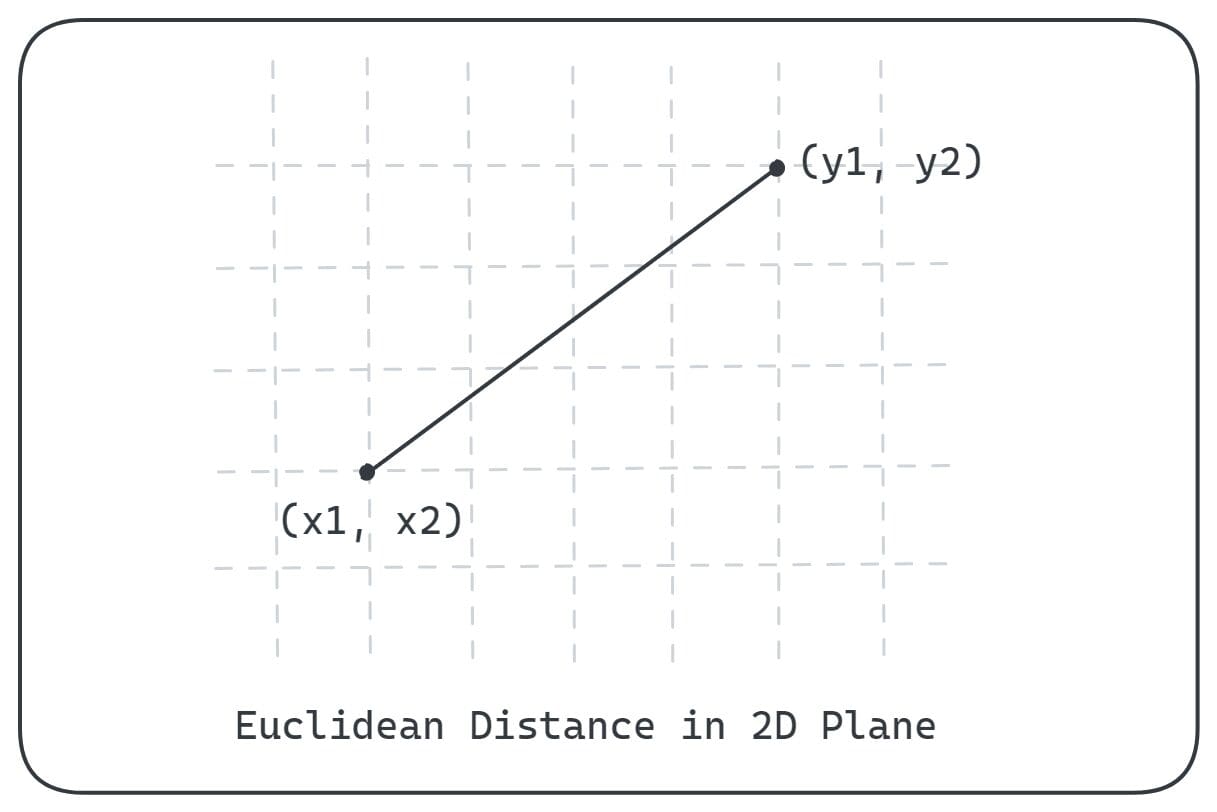
Euclidean distance is the shortest distance between any two factors in a metric house. Think about two factors x and y in a two-dimensional aircraft with coordinates (x1, x2) and (y1, y2), respectively.
The Euclidean distance between x and y is proven:
Picture by Writer
This distance is given by the sq. root of the sum of the squared variations between the corresponding coordinates of the 2 factors. Mathematically, the Euclidean distance between the factors x and y in two-dimensional aircraft is given by:

Extending to n dimensions, the factors x and y are of the shape x = (x1, x2, …, xn) and y = (y1, y2, …, yn), now we have the next equation for Euclidean distance:

Computing Euclidean Distance in Python
The Euclidean distance and the opposite distance metrics in that article will be computed utilizing comfort capabilities from the spatial module in SciPy.
As a primary step, let’s import distance from Scipy’s spatial module:
from scipy.spatial import distance
We then initialize two factors x and y like so:
We are able to use the euclidean comfort perform to search out the Euclidean distance between the factors x and y:
print(distance.euclidean(x,y))
Output >> 10.198039027185569
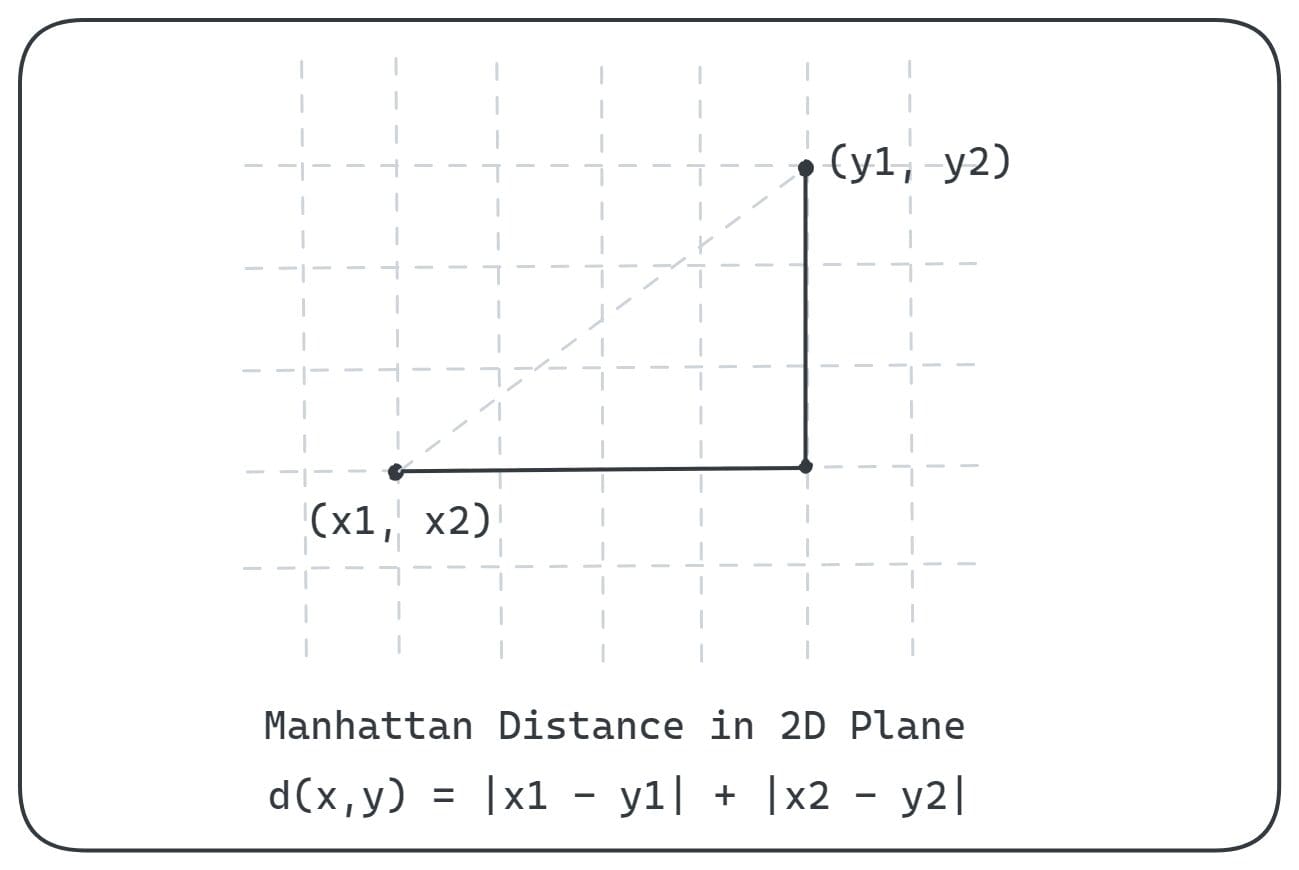
The Manhattan distance, additionally referred to as taxicab distance or cityblock distance, is one other widespread distance metric. Suppose you’re inside a two-dimensional aircraft and you’ll transfer solely alongside the axes as proven:
Picture by Writer
The Manhattan distance between the factors x and y is given by:

In n-dimensional house, the place every level has n coordinates, the Manhattan distance is given by:

Although the Manhattan distance doesn’t give the shortest distance between any two given factors, it’s typically most popular in purposes the place the characteristic factors are situated in a high-dimensional house [3].
Computing Manhattan Distance in Python
We retain the import and x and y from the earlier instance:
from scipy.spatial import distance
x = [3,6,9]
y = [1,0,1]
To compute the Manhattan (or cityblock) distance, we are able to use the cityblock perform:
print(distance.cityblock(x,y))
Output >> 16
Named after the German mathematician, Hermann Minkowski [2], the Minkowski distance in a normed vector house is given by:

It’s fairly easy to see that for p = 1, the Minkowski distance equation takes the identical kind as that of Manhattan distance:

Equally, for p = 2, the Minkowski distance is equal to the Euclidean distance:
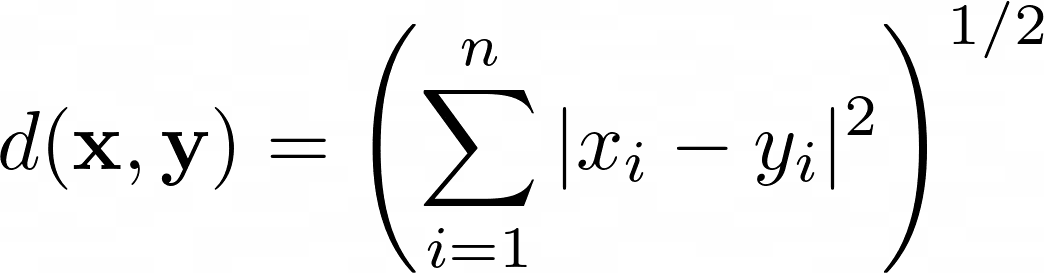
Computing Minkowski Distance in Python
Let’s compute the Minkowski distance between the factors x and y:
from scipy.spatial import distance
x = [3,6,9]
y = [1,0,1]
Along with the factors (arrays) between which the gap is to be calculated, the minkowski perform to compute the gap additionally takes within the parameter p:
print(distance.minkowski(x,y,p=3))
Output >> 9.028714870948003
To confirm if Minkowski distance evaluates to Manhattan distance for p =1, let’s name minkowski perform with p set to 1:
print(distance.minkowski(x,y,p=1))
Output >> 16.0
Let’s additionally confirm that Minkowski distance for p = 2 evaluates to the Euclidean distance we computed earlier:
print(distance.minkowski(x,y,p=2))
Output >> 10.198039027185569
And that’s a wrap! Should you’re conversant in normed vector areas, you must have the ability to see similarity between the gap metrics mentioned right here and Lp norms. The Euclidean, Manhattan, and Minkowski distances are equal to the L2, L1, and Lp norms of the distinction vector in a normed vector house.
That is all for this tutorial. I hope you’ve now gotten the hold of the frequent distance metrics. As a subsequent step, you may attempt taking part in round with the totally different metrics you’ve realized the subsequent time you prepare machine studying algorithms.
Should you’re trying to get began with knowledge science, take a look at this list of GitHub repositories to learn data science. Pleased studying!
[1] Metric Spaces, Wolfram Mathworld
[2] Minkowski Distance, Wikipedia
[3] On the Surprising Behavior of Distance Metrics in High Dimensional Space, CC Agarwal et al.
[4] SciPy Distance Functions, SciPy Docs
Bala Priya C is a technical author who enjoys creating long-form content material. Her areas of curiosity embody math, programming, and knowledge science. She shares her studying with the developer neighborhood by authoring tutorials, how-to guides, and extra.
[ad_2]
Source link



