Performing a T-Test in Python

Picture by Editor

Key Takeaways

• The t-test is a statistical check that can be utilized to find out if there’s a vital distinction between the technique of two unbiased samples of information.
• We illustrate how a t-test may be utilized utilizing the iris dataset and Python’s Scipy library.

The t-test is a statistical check that can be utilized to find out if there’s a vital distinction between the technique of two unbiased samples of information. On this tutorial, we illustrate probably the most fundamental model of the t-test, for which we’ll assume that the 2 samples have equal variances. Different superior variations of the t-test embody the Welch’s t-test, which is an adaptation of the t-test, and is extra dependable when the 2 samples have unequal variances and presumably unequal pattern sizes.

The t statistic or t-value is calculated as follows:

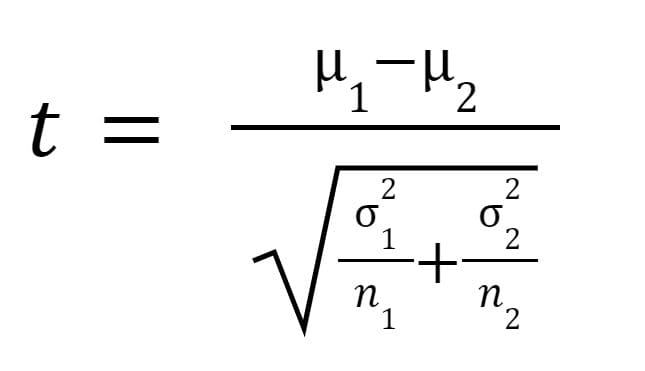
the place is the imply of pattern 1, is the imply of pattern 2, is the variance of pattern 1, is the variance of pattern 2, is the pattern dimension of pattern 1, and is the pattern dimension of pattern 2.

As an instance using the t-test, we’ll present a easy instance utilizing the iris dataset. Suppose we observe two unbiased samples, e.g. flower sepal lengths, and we’re contemplating whether or not the 2 samples have been drawn from the identical inhabitants (e.g. the identical species of flower or two species with related sepal traits) or two completely different populations.

The t-test quantifies the distinction between the arithmetic technique of the 2 samples. The p-value quantifies the likelihood of acquiring the noticed outcomes, assuming the null speculation (that the samples are drawn from populations with the identical inhabitants means) is true. A p-value bigger than a selected threshold (e.g. 5% or 0.05) signifies that our statement just isn’t so unlikely to have occurred by likelihood. Due to this fact, we settle for the null speculation of equal inhabitants means. If the p-value is smaller than our threshold, then we now have proof in opposition to the null speculation of equal inhabitants means.

T-Check Enter

The inputs or parameters vital for performing a t-test are:

• Two arrays a and b containing the info for pattern 1 and pattern 2

T-Check Outputs

The t-test returns the next:

• The calculated t-statistics
• The p-value

Import vital libraries

import numpy as np
from scipy import stats 
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

Load Iris Dataset

from sklearn import datasets
iris = datasets.load_iris()
sep_length = iris.information[:,0]
a_1, a_2 = train_test_split(sep_length, test_size=0.4, random_state=0)
b_1, b_2 = train_test_split(sep_length, test_size=0.4, random_state=1)

Calculate the pattern means and pattern variances

mu1 = np.imply(a_1)
 
mu2 = np.imply(b_1)
 
np.std(a_1)
 
np.std(b_1)

Implement t-test

stats.ttest_ind(a_1, b_1, equal_var = False)

Output 

Ttest_indResult(statistic=0.830066093774641, pvalue=0.4076270841218671)

stats.ttest_ind(b_1, a_1, equal_var=False)

Output 

Ttest_indResult(statistic=-0.830066093774641, pvalue=0.4076270841218671)

stats.ttest_ind(a_1, b_1, equal_var=True)

Output

Ttest_indResult(statistic=0.830066093774641, pvalue=0.4076132965045395)

Observations

We observe that the utilizing “true” or “false” for the “equal-var” parameter doesn’t change the t-test outcomes that a lot. We additionally observe that interchanging the order of the pattern arrays a_1 and b_1 yields a adverse t-test worth, however doesn’t change the magnitude of the t-test worth, as anticipated. For the reason that calculated p-value is means bigger than the edge worth of 0.05, we are able to reject the null speculation that the distinction between the technique of pattern 1 and pattern 2 are vital. This exhibits that the sepal lengths for pattern 1 and pattern 2 have been drawn from identical inhabitants information.

a_1, a_2 = train_test_split(sep_length, test_size=0.4, random_state=0)
b_1, b_2 = train_test_split(sep_length, test_size=0.5, random_state=1)

Calculate the pattern means and pattern variances

mu1 = np.imply(a_1)
 
mu2 = np.imply(b_1)
 
np.std(a_1)
 
np.std(b_1)

Implement t-test

stats.ttest_ind(a_1, b_1, equal_var = False)

Output

stats.ttest_ind(a_1, b_1, equal_var = False)

Observations

We observe that utilizing samples with unequal dimension doesn’t change the t-statistics and p-value considerably. 
 

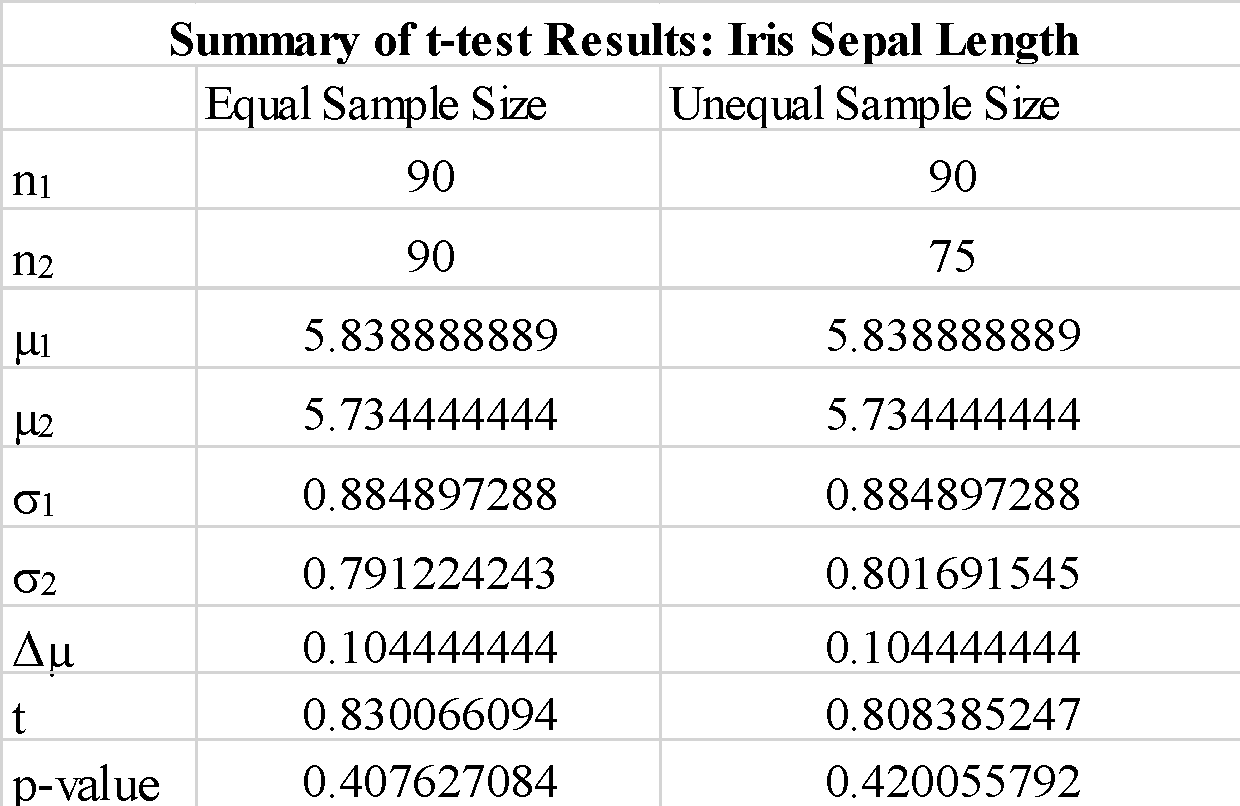
In abstract, we’ve proven how a easy t-test could possibly be carried out utilizing the scipy library in python.
 
 
Benjamin O. Tayo is a Physicist, Information Science Educator, and Author, in addition to the Proprietor of DataScienceHub. Beforehand, Benjamin was instructing Engineering and Physics at U. of Central Oklahoma, Grand Canyon U., and Pittsburgh State U.