[ad_1]
1.1 The constructing blocks of the mannequin
To grasp what sARIMA fashions are, let’s first introduce the constructing blocks of those fashions.
sARIMA is a composition of various sub-models (i.e. polynomials that we use to symbolize our time collection information) which type the acronym: seasonal (s) autoregressive (AR) built-in (I) transferring common (MA):
- AR: the autoregressive element, ruled by the hyperparameter “p”, assumes that the present worth at a time “t” will be expressed as a linear mixture of the earlier “p” values:
- I: the built-in element is represented by the hyperparameter “d”, which is the diploma of the differencing transformation utilized to the info. Differencing is a method used to take away pattern from the info (i.e. make the info stationary with respect to the imply, as we’ll see later), which helps the mannequin match the info because it isolates the pattern element (we use d=1 for linear pattern, d=2 for quadratic pattern, …). Differencing the info with d=1 means working with the distinction between consecutive information factors:
- MA: the transferring common element, ruled by the hyperparameter “q”, assumes that the present worth at a time “t” will be expressed as a relentless time period (normally the imply) plus a linear mixture of the errors of the earlier “q” factors:
- If we contemplate the parts up to now, we get “ARIMA”, which is the identify of a mannequin household to work with time collection information with no seasonality. sARIMA fashions are a generalization to work with seasonal information with the addition of an S-component: the seasonal element, which consists of a brand new set of AR, I, MA parts with a seasonal lag. In different phrases, as soon as recognized a seasonality and outlined its lag (represented by the hyperparameter “m” — e.g. m=12 implies that yearly, on a month-to-month dataset, we see the identical conduct), we create a brand new set of AR (P), I (D), MA (Q) parts, with respect to the seasonal lag (m) (e.g. if D=1 and m=12, because of this we apply a 1-degree differencing to the collection, with a lag of 12).
To sum up, the sARIMA mannequin is outlined by 7 hyperparameters: 3 for the non-seasonal a part of the mannequin, and 4 for the seasonal half. They’re indicated as:
sARIMA (p,d,q) (P,D,Q)m
Due to the mannequin flexibility, we are able to “swap off” the parts that aren’t embodied in our information (i.e. if the info doesn’t have a pattern or doesn’t have seasonality, the respective parameters will be set to 0) and nonetheless use the identical mannequin framework to suit the info.
Alternatively, amongst sARIMA limitations, we have now that these fashions can seize just one seasonality. If a day by day dataset has a yearly plus a weekly seasonality, we’ll want to decide on the strongest one.
1.2 How to decide on the mannequin hyperparameters: ACF and PACF
To determine the mannequin hyperparameters, we usually take a look at the autocorrelation and partial-autocorrelation of the time collection; since all of the above parts use previous information to mannequin current and future factors, we must always examine how previous and current information are correlated and outline what number of previous information factors we want, to mannequin the current.
For that reason, autocorrelation and partial-autocorrelation are two broadly used features:
- ACF (autocorrelation): describes the correlation of the time collection, with its lags. All information factors are in comparison with their earlier lag 1, lag 2, lag 3, … The ensuing correlation is plotted on a histogram. This chart (additionally referred to as “correlogram”) is used to visualise how a lot info is retained all through the time collection. The ACF helps us in selecting the sARIMA mannequin as a result of:
The ACF helps to determine the MA(q) hyperparameter.
- PACF (partial autocorrelation): describes the partial correlation of the time collection, with its lags. In another way from the ACF, the PACF reveals the correlation between some extent X_t and a lag, which isn’t defined by widespread correlations with different lags at a decrease order. In different phrases, the PACF isolates the direct correlation between two phrases. The PACF helps us in selecting the sARIMA mannequin as a result of:
The PACF helps to determine the AR(p) hyperparameter.
Earlier than utilizing these instruments, nevertheless, we have to point out that ACF and PACF can solely be used on a “stationary” time collection.
1.3 Stationarity
A (weakly) stationary time collection is a time collection the place:
- The imply is fixed over time (i.e. the collection fluctuates round a horizontal line with out constructive or detrimental traits)
- The variance is fixed over time (i.e. there isn’t a seasonality or change within the deviation from the imply)
After all not all time collection are natively stationary; nevertheless, we are able to rework them to make them stationary. The commonest transformations used to make a time collection stationary are:
- The pure log: by making use of the log to every information level, we normally handle to make the time collection stationary with respect to the variance.
- Differencing: by differencing a time collection, we normally handle to take away the pattern and make the time collection stationary with respect to the imply.
After remodeling the time collection, we are able to use two instruments to verify that it’s stationary:
- The Field-Cox plot: it is a plot of the rolling imply (on the x-axis) vs the rolling normal deviation (on the y-axis) (or the imply vs variance of grouped factors). Our information is stationary if we don’t observe any explicit traits within the chart and we see little variation on each axes.
- The Augmented Dickey–Fuller take a look at (ADF): a statistical take a look at wherein we attempt to reject the null speculation stating that the time collection is non-stationary.
As soon as a time collection is stationary, we are able to analyze the ACF and PACF patterns, and discover the SARIMA mannequin hyperparameters.
Figuring out the sARIMA mannequin that matches our information encompass a collection of steps, which we are going to carry out on the AirPassenger dataset (obtainable here).
Every step roughly corresponds to a “web page” of the Sprint net app.
2.1 Plot your information
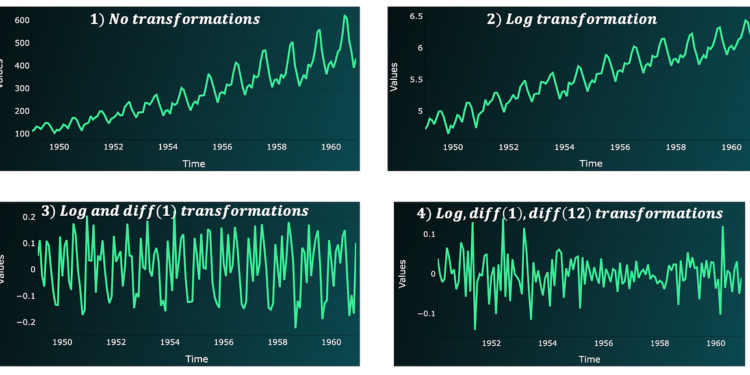
Create a line chart of your uncooked information: among the options described above will be seen by the bare eye, particularly stationarity, and seasonality.
Within the above chart, we see a constructive linear pattern and a recurrent seasonality sample; contemplating that we have now month-to-month information, we are able to assume the seasonality to be yearly (lag 12). The information just isn’t stationary.
2.2 Rework the info to make it stationary
With a purpose to discover the mannequin hyperparameters, we have to work with a stationary time collection. So, if the info just isn’t stationary, we’ll want to remodel it:
- Begin with the log transformation, to make the info stationary with respect to the variance (the log is outlined over constructive values. So, if the info presents detrimental or 0 values, add a relentless to every datapoint).
- Apply differencing to make the info stationary with respect to the imply. Often begin with differencing of order 1 and lag 1. Then, if information remains to be not stationary, strive differencing with respect to the seasonal lag (e.g. 12 if we have now month-to-month information). (Utilizing a reverse order gained’t make a distinction).
With our dataset, we have to carry out the next steps to make it totally stationary:
After every step, by wanting on the ADF take a look at p-value and Field-Cox plot, we see that:
- The Field-Cox plot will get progressively cleaned from any pattern and all factors get nearer and nearer.
- The p-value progressively drops. We are able to lastly reject the null speculation of the take a look at.
2.3 Determine appropriate mannequin hyperparameters with the ACF and PACF
Whereas remodeling the info to stationary, we have now already recognized 3 parameters:
- Since we utilized differencing, the mannequin will embody differencing parts. We utilized a differencing of 1 and 12: we are able to set d=1 and D=1 with m=12 (seasonality of 12).
For the remaining parameters, we are able to take a look at the ACF and PACF after the transformations.
Generally, we are able to apply the next guidelines:
- We’ve got an AR(p) course of if: the PACF has a major spike at a sure lag “p” (and no important spikes after) and the ACF decays or reveals a sinusoidal conduct (alternating constructive, detrimental spikes).
- We’ve got a MA(q) course of if: the ACF has a major spike at a sure lag “q” (and no important spikes after) and the PACF decays or reveals a sinusoidal conduct (alternating constructive, detrimental spikes).
- Within the case of seasonal AR(P) or MA(Q) processes, we are going to see that the numerous spikes repeat on the seasonal lags.
By taking a look at our instance, we see the next:
- The closest rule to the above conduct, suggests some MA(q) course of with “q” between 1 and three; the truth that we nonetheless have a major spike at 12, can also recommend an MA(Q) with Q=1 (since m=12).
We use the ACF and PACF to get a variety of hyperparameter values that may type mannequin candidates. We are able to examine these completely different mannequin candidates towards our information, and decide the top-performing one.
Within the instance, our mannequin candidates appear to be:
- SARIMA (p,d,q) (P,D,Q)m = (0, 1, 1) (0, 1, 1) 12
- SARIMA (p,d,q) (P,D,Q)m = (0, 1, 3) (0, 1, 1) 12
2.4 Carry out a mannequin grid search to determine optimum hyperparameters
Grid search can be utilized to match a number of mannequin candidates towards one another: we match every mannequin to the info and decide the top-performing one.
To arrange a grid search we have to:
- create a listing with all attainable combos of mannequin hyperparameters, given a variety of values for every hyperparameter.
- match every mannequin and measure its efficiency utilizing a KPI of selection.
- choose the hyperparameters wanting on the top-performing fashions.
In our case, we are going to examine mannequin performances utilizing the AIC (Akaike info criterion) rating. This KPI system consists of a trade-off between the becoming error (accuracy) and mannequin complexity. Generally, when the complexity is just too low, the error is excessive, as a result of we over-simplify the mannequin becoming activity; quite the opposite, when complexity is just too excessive, the error remains to be excessive resulting from overfitting. A trade-off between these two will permit us to determine the “top-performing” mannequin.
Sensible notice: with becoming a sARIMA mannequin, we might want to use the unique dataset with the log transformation (if we’ve utilized it), however we don’t wish to use the info with differencing transformations.
We are able to select to order a part of the time collection (normally the latest 20% observations) as a take a look at set.
In our instance, based mostly on the beneath hyperparameter ranges, the most effective mannequin is:
SARIMA (p,d,q) (P,D,Q)m = (0, 1, 1) (0, 1, 1) 12
2.5 Remaining mannequin: match and predictions
We are able to lastly predict information for practice, take a look at, and any future out-of-sample statement. The ultimate plot is:
To substantiate that we captured all correlations, we are able to plot the mannequin residuals ACF and PACF:
On this case, some sign from the sturdy seasonality element remains to be current, however many of the remaining lags have a 0 correlation.
The steps described above ought to work on any dataset which might be modeled by sARIMA. To recap :
1-Plot & discover your information
2-Apply transformations to make the info stationary (give attention to the left-end charts and the ADF take a look at)
3-Determine appropriate hyperparameters by wanting on the ACF and PACF (right-end charts)
4-Carry out a grid search to pick out optimum hyperparameters
5-Match and predict utilizing the most effective mannequin
Obtain the app domestically, add your individual datasets (by changing the .csv file within the information folder) and attempt to match the most effective mannequin.
Thanks for studying!
[ad_2]
Source link