[ad_1]

Picture by Writer
Earlier than we begin to find out about Chebychev’s theorem, it will likely be helpful to have a great understanding of the Empirical rule.
The Empirical rule tells you the place many of the values lie in a traditional distribution. It states that:
- round 68% of the info lie inside 1 customary deviation of the imply
- round 95% of the info lie inside 2 customary deviations of the imply
- round 99.7% of the info lie inside 3 customary deviations of the imply
Nonetheless, you may by no means be 100% certain that the distribution of information will comply with a traditional bell curve. Once you’re working with datasets, it’s best to all the time ask in case your information is skewed. That is the place Chebychev’s theorem comes into play.
Chebyshev’s Theorem was confirmed by Russian mathematician Pafnuty Chebyshev and sometimes known as Chebyshev’s Inequality. It may be utilized to any dataset, particularly ones which have a variety of chance distributions that don’t comply with the traditional distribution all of us need.
In Layman’s phrases, it states that solely a sure share of observations will be greater than a sure distance from the imply.
For Chebychev’s Theorem, it states that when utilizing any numerical dataset:
- A minimal of three/4 of the info lie inside 2 customary deviations of the imply
- A minimal of 8/9 of the info lie inside 3 customary deviations of the imply
- 1−1 ∕ k2 of the info lies inside ok customary deviations of the imply
The phrase ‘a minimal’ is used as a result of the theory offers the minimal proportion of information that lies inside a given variety of customary deviations of the imply.
The picture beneath visually exhibits you the distinction between the Empirical Rule and Chebyshev’s Theorem:
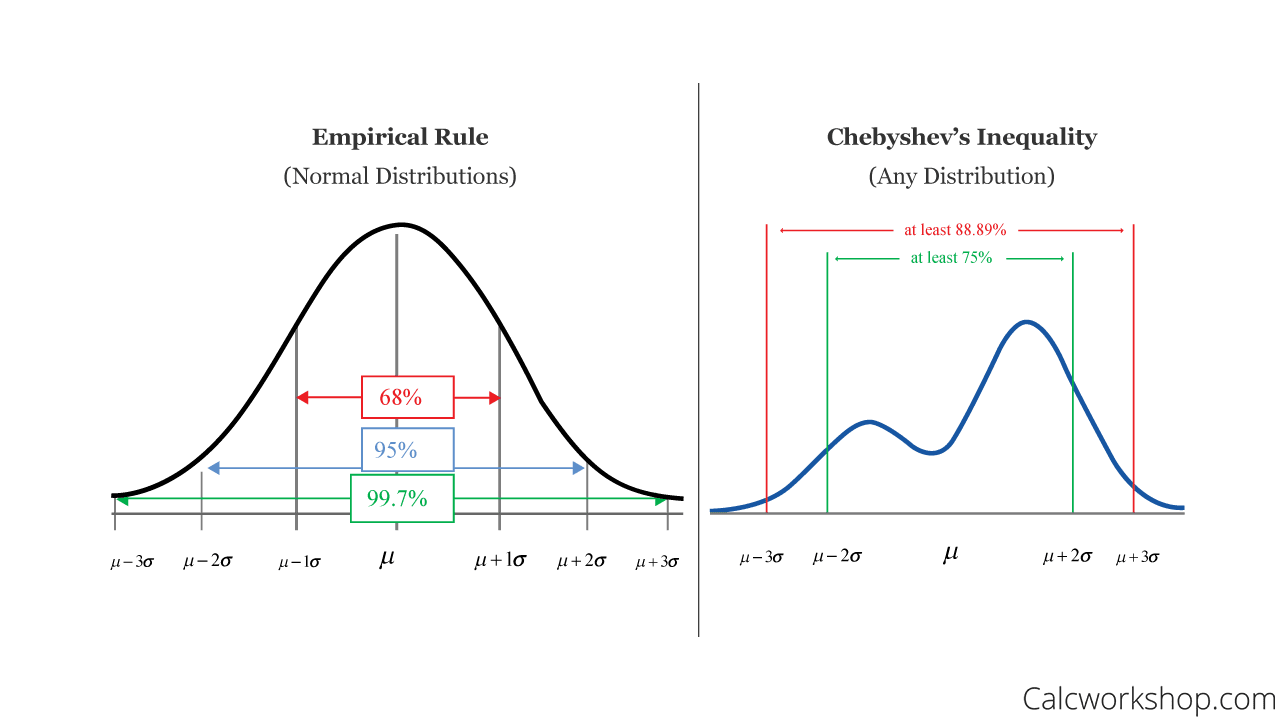
Supply: calcworkshop
The equation for Chebyshev’s Theorem:
There are two methods of presenting Chebyshev’s theorem:
X is a random variable
μ is the imply
σ is the usual deviation
ok>0 is a optimistic quantity
- P(|X – μ| ≥ kσ) ≤ 1 / k2
The equation states that the chance that X falls greater than ok customary deviations away from the imply is at most 1/k2. This may also be written like this:
- P(|X – μ| ≤ kσ) ≥ 1 – 1 / k2
Chebyshev’s Theorem implies that it is extremely unlikely {that a} random variable will likely be removed from the imply. Subsequently, the k-value we use is the restrict we set for the variety of customary deviations away from the imply.
Chebyshev’s theorem can be utilized when ok >1
In Knowledge Science, you utilize a whole lot of statistical measures to be taught extra concerning the dataset you might be working with. The imply calculates the central tendency of an information set, nonetheless, this doesn’t inform us sufficient concerning the dataset.
As a Knowledge Scientist, you can be questioning to be taught extra concerning the dispersion of the info. And with the intention to determine this out might want to measure the usual deviation, which represents the distinction between every worth and the imply. When you may have the imply and the usual deviation, you may be taught so much a couple of dataset.
The extra variance we have now, the extra unfold the distribution of information factors is away from the imply, and the decrease the variance, the much less unfold the distribution of information factors is away from the imply.
If a random variable has low variance, then the noticed values will likely be grouped near the imply. As proven within the picture beneath, this ends in a smaller customary deviation. Nonetheless, in case your distribution of information has a big variance, then your observations will naturally be extra unfold out and additional away from the imply. As proven within the picture beneath, this ends in a bigger customary deviation.
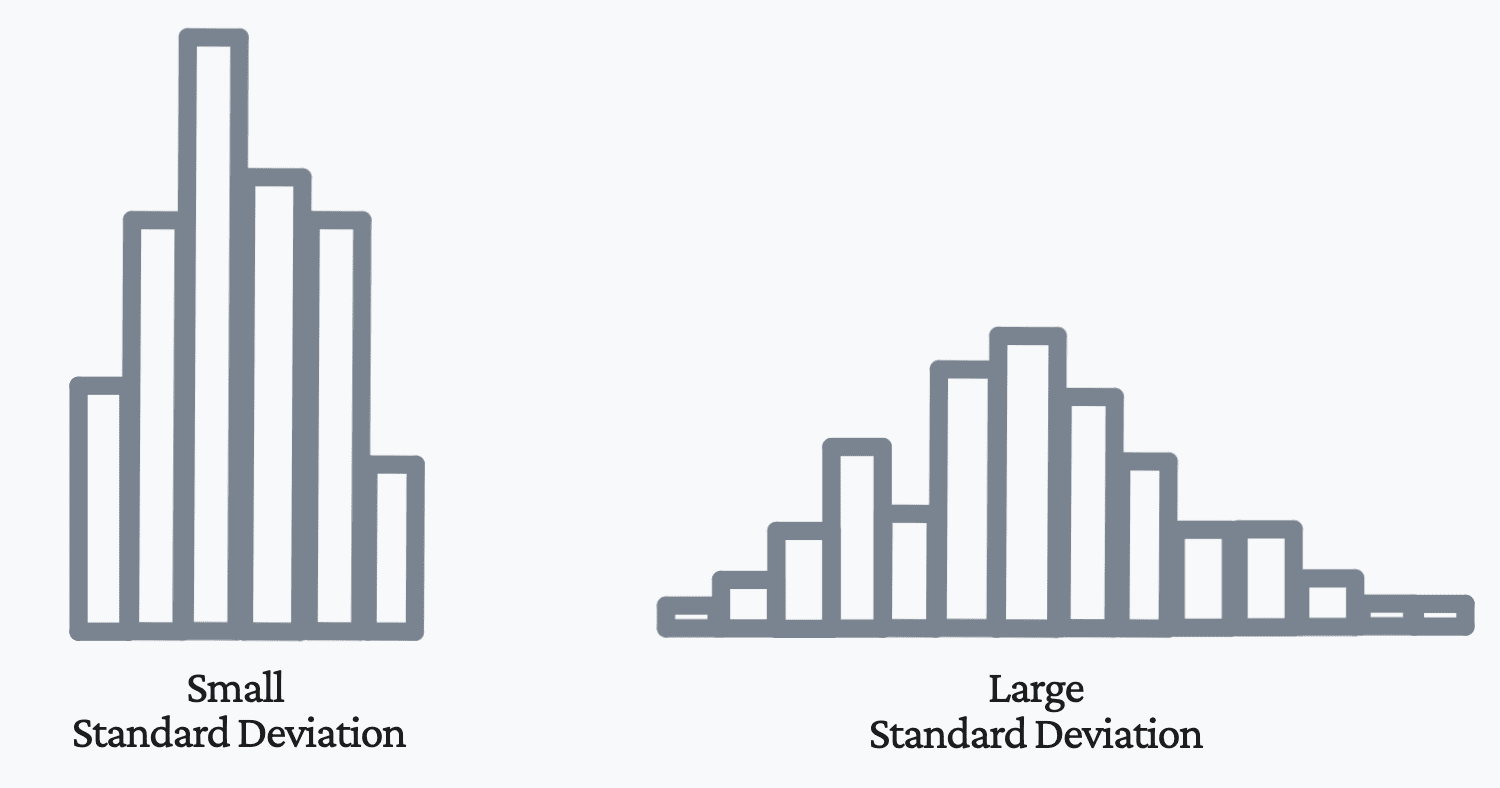
Picture by Writer
Knowledge Scientists and different tech consultants will come throughout datasets which have a big variance. Subsequently, their common go-to Empirical rule gained’t assist them they usually should use Chebyshev’s theorem.
If you wish to be taught extra concerning the dispersion of your information factors, so long as you may have calculated the imply and customary deviation and it doesn’t comply with a traditional distribution, Chebyshev’s theorem will be utilized. Will probably be capable of decide the proportion of information falling inside a selected vary of the imply.
Nisha Arya is a Knowledge Scientist and Freelance Technical Author. She is especially interested by offering Knowledge Science profession recommendation or tutorials and concept primarily based information round Knowledge Science. She additionally needs to discover the other ways Synthetic Intelligence is/can profit the longevity of human life. A eager learner, looking for to broaden her tech information and writing expertise, while serving to information others.
[ad_2]
Source link



